幺正费米气体

介绍

幺正费米气体模型描述了具有无限大 s 波散射长度的双组分费米气体。 由于 s 波相互作用在低温主导，因此我们通常可以忽略 p 波相互作用等。 另一种等效的观点是将它们视为具有内部自旋自由度的相同费米子。 费米子在碰撞过程中无法翻转自旋。如果我们将它们标记为自旋向上和自旋向下。这两者是等效的，我们甚至可以在布洛赫球上旋转自旋向上和自旋向下而不改变哈密顿量。 因此，我们可以将其称为 SU(2) 费米气体。

幺正费米气体在核物理和天体物理中的应用

中子星的地壳 或原子核的核心

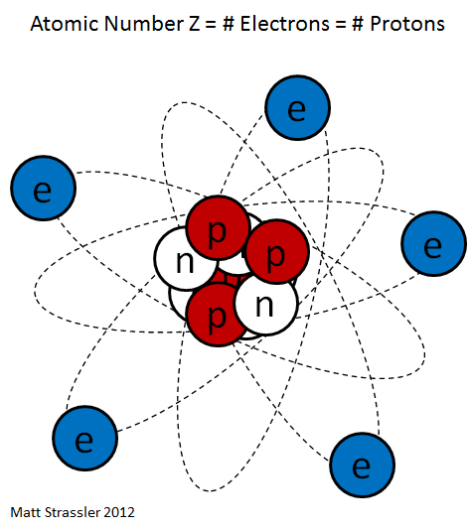
可以用幺正费米气体近似。

尺度不变性

考虑一个没有外部势的均匀系统，系统唯一可能具有的长度来自相互作用。 在低温下，s 波相互作用可以通过散射长度和有效范围来描述。 在极低温或稀释极限下，我们甚至可以忽略有效范围。 这个系统有两个特殊点，零散射长度，对应于无相互作用系统，和无限散射长度，对应于幺正费米气体。 在这两个极限下，系统具有尺度不变性。这意味着，如果你扩展或缩小系统，只需将一个缩放因子乘以原始哈密顿量。

原子物理学: 费什巴赫共振

我们可以使用 费什巴赫共振 来调节冷原子的散射长度，从弱相互作用系统到幺正费米气体。 例如，\(^6\)Li 的基态 \(^2\)S\(_{1/2}\) 有 6 个超精细态。

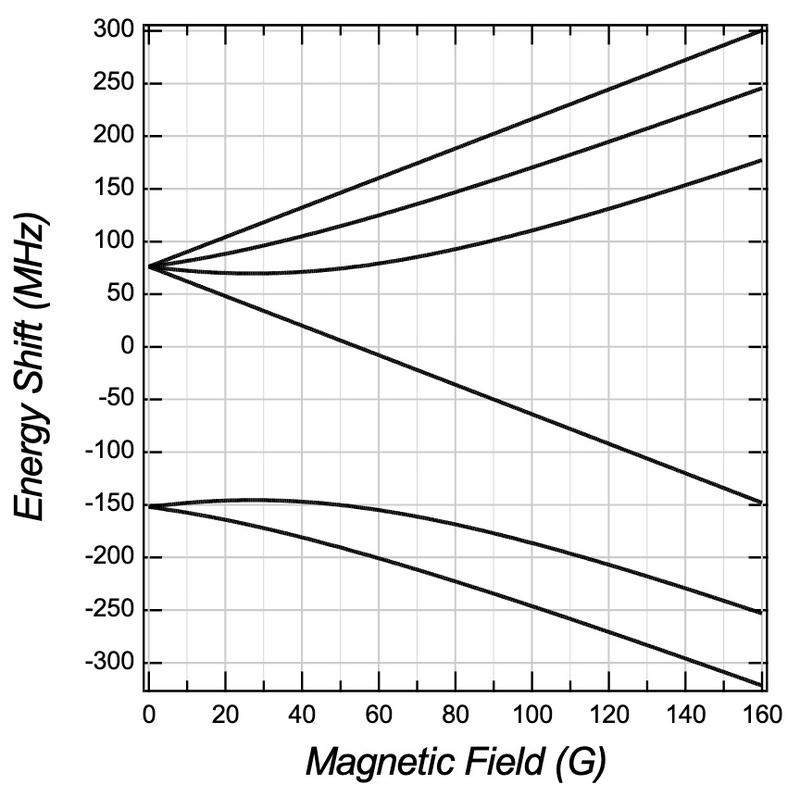
选择其中两个，并将磁场调节到某个魔法数字，散射长度可以调节到无限。

热力学

我们考虑一个化学势固定的巨正则系综。 幺正费米气体的状态方程可以通过考虑高温展开得到。这个展开称为 维里展开。请参阅 X.-J. Liu, Phys. Rep. 524, 37 (2013) 以获取综述。

展开系数称为维里系数。

四阶维里系数

我们使用 路径积分蒙特卡罗(PIMC) 方法来确定四阶维里系数。 下图显示了谐振子陷阱中维里系数随逆温度的变化。

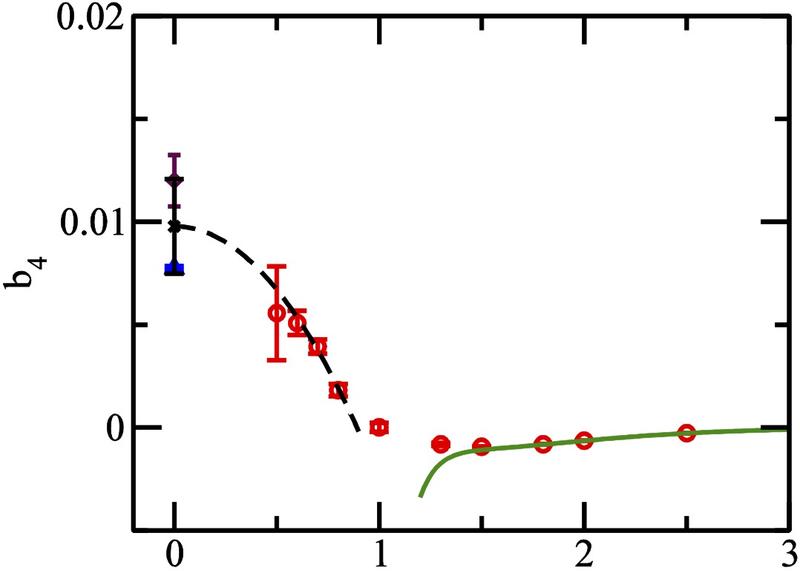
在低温下，系数已知为负值（绿色）。 在高温下，系数从实验中拟合为正值。 PIMC 成功地计算了中间温度范围内的维里系数，并表明理论与实验之间没有冲突。