路径积分蒙特卡罗方法
费曼提出使用经典计算机模拟量子系统的想法。
介绍
路径积分蒙特卡罗(PIMC)方法是一种数值有限温度方法,可以处理从少数粒子到数百粒子的系统。它已广泛应用于许多不同的物理领域,如凝聚态系统、纳米线、范德华簇、量子点、核物质、冷原子等。例如,块状氦的超流性首次通过PIMC技术得到了数值验证。许多其他玻色子系统的热力学量,如内能、热容、密度分布和对关联函数也可以精确计算。尽管文献中主要处理的是玻色子统计,但也可以处理费米子统计系统。在低温下,费米符号问题使得模拟变得困难,但至少对于某些费米子系统,我们可以在接近或处于量子简并状态的温度下进行处理,而不会遇到符号问题。
下面我们给出一个关于单粒子在谐振子陷阱中的PIMC计算的简单示例。
谐振子陷阱中的单粒子 - 本征态基底
对于一个由哈密顿量\(\mathcal{H}\)描述的谐振子陷阱中的单粒子,
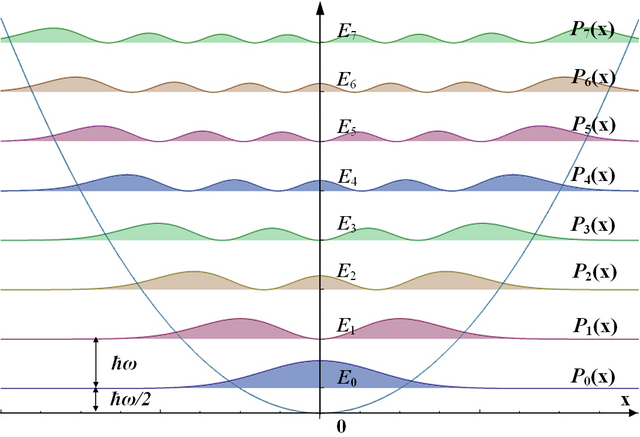
\[\mathcal{H}=-\frac{\hbar^2}{2m}\frac{\partial^2}{\partial x^2}+\frac{1}{2}m \omega^2 x^2,\]其中\(\hbar\)、\(m\)和\(\omega\)分别是约化普朗克常数、粒子质量和角频率,我们可以计算本征能量\(E_j\)和本征函数\(\psi_j\)。对所有允许状态进行Boltzmann加权\(e^{-E_j/k_BT}\)的热平均可以得到有限温度性质。虽然单粒子谐振子问题简单到可以通过这种“蛮力”方法解决,但当我们考虑两个、三个……带有相互作用的粒子时,问题就变得更加困难甚至不可能。左图(引自维基百科)展示了单粒子在谐振子陷阱中的本征值和本征函数的平方。
密度矩阵和Trotter公式
现在我们介绍考虑有限温度的路径积分方法。密度矩阵\(\rho(x,x',\beta)\),
\[\rho(x,x',\beta)=\bra{x}\exp(-\beta \mathcal{H})\ket{x'},\]其中\(\beta=1/(k_BT)\)是逆温度(或“虚时间”),是我们可以用来计算几乎所有热力学量的关键量。Trotter公式为
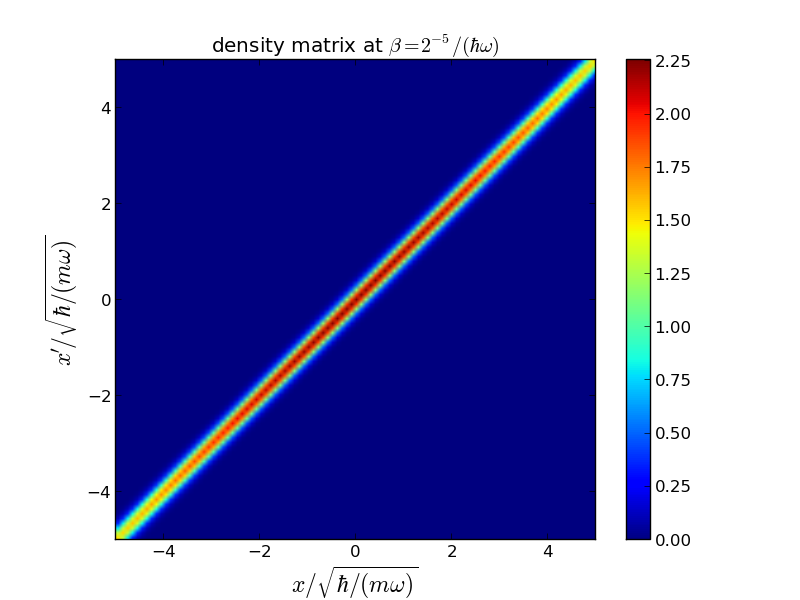
\[e^{-\beta (\mathcal{K}+\mathcal{V})}= e^{-\beta\mathcal{V/2}}e^{-\beta\mathcal{K}}e^{-\beta\mathcal{V/2}} +O(\beta^3),\]其中\(\mathcal{K}\)和\(\mathcal{V}\)分别是动能和势能算符。密度矩阵在高温下可以较为准确地近似,但在低温下则不行。左图显示了在相对高温下的密度矩阵,即在\(\beta=\frac{1}{32}\hbar\omega\)时的情况。
密度矩阵的卷积
利用密度矩阵的卷积性质,
\[\rho(x_0,x_2,\beta)=\int dx_1 \rho(x_0,x_1,\beta/2)\rho(x_1,x_2,\beta/2),\]我们可以将低温(小\(\beta\))下的密度矩阵表示为高温(大\(\beta\))下两个密度矩阵的乘积。代价是需要对\(x\)进行额外积分。另一种理解方法是插入完整的坐标基底:
\[\rho(x_0,x_2,\beta)=\int dx_1 \bra{x_0}\exp(-\beta \mathcal{H}/2)\ket{x_1}\bra{x_1}\exp(-\beta \mathcal{H}/2)\ket{x_2}.\]为了获得准确的模拟结果,我们必须插入足够多的中间位置基底,即我们必须进行足够多的“辅助积分”,
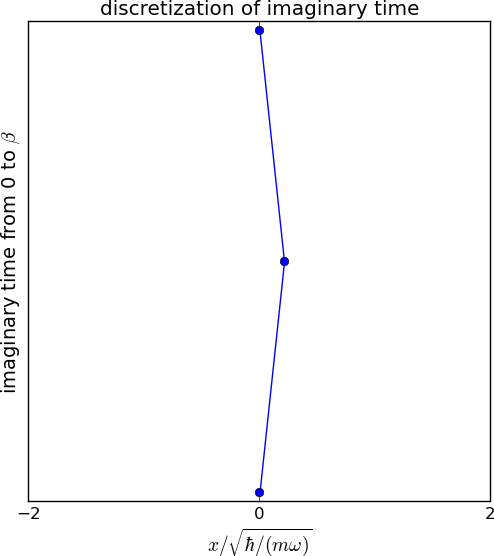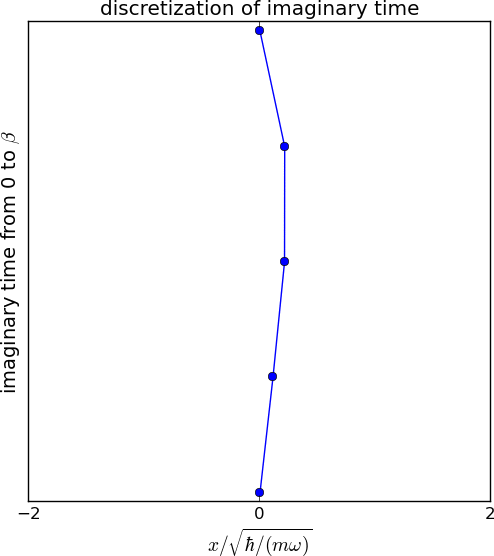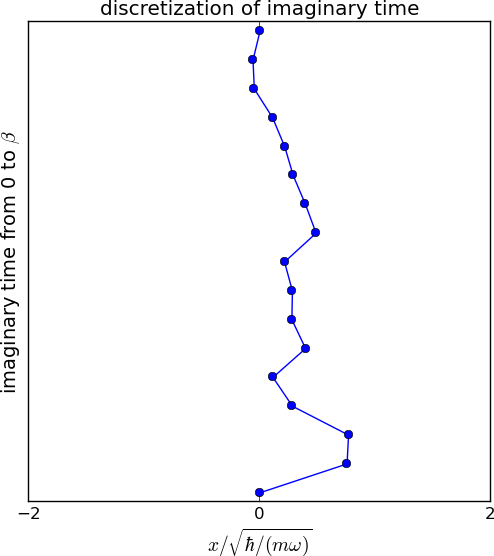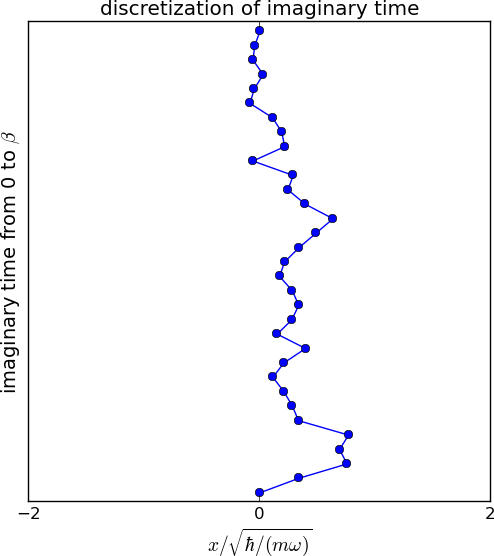
\[\rho(x_0,x_M,\beta)=\int dx_1\dots\int dx_{M-1} \bra{x_0}\exp(-\beta \mathcal{H}/M)\ket{x_1}\dots\\\bra{x_{M-1}}\exp(-\beta \mathcal{H}/M)\ket{x_M}.\]时间片数\(M\)取决于所需的精度。左图展示了虚时间的离散化。点和连线分别表示位置基底和密度矩阵。在最后的图中,\(M\)为32,即我们插入了31个中间点。多维积分可以使用蒙特卡罗技术进行评估。
朴素路径积分蒙特卡罗
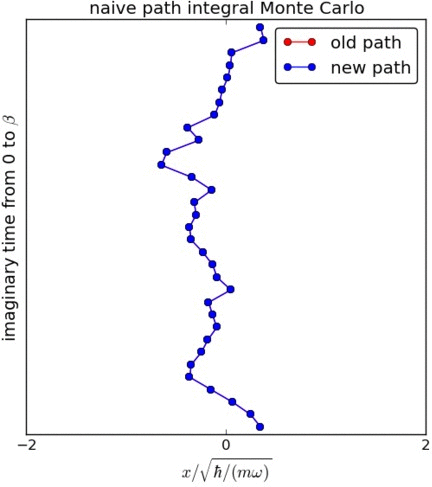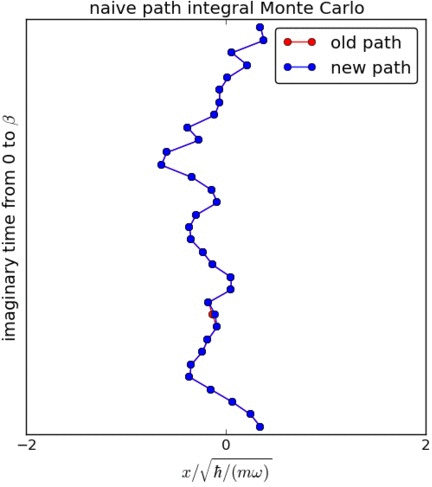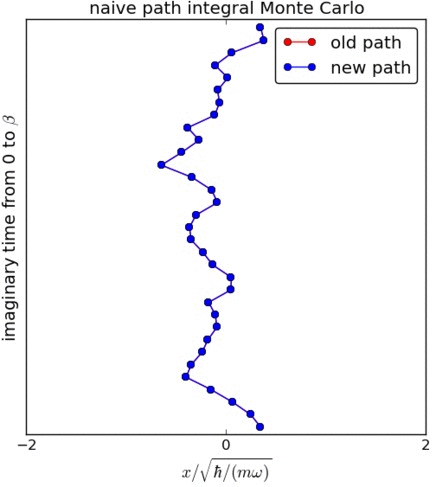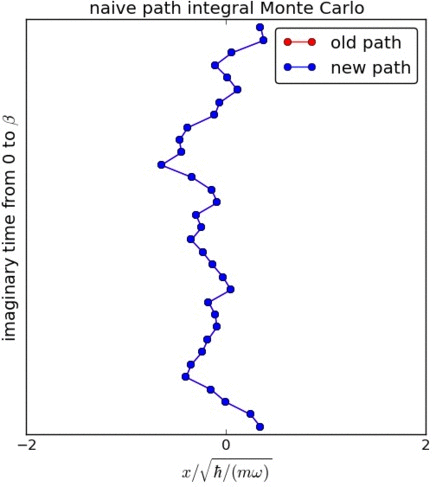
为了计算粒子的密度分布,我们只需要密度矩阵的对角元素。这对应于\(x_M=x_0\),即路径是闭合的,可以看作一个环。我们使用马尔可夫链对路径进行采样。为了更新路径,我们计算由新路径表示的密度矩阵与旧路径表示的密度矩阵之比\(p\)。接受路径的概率由\(p\)决定(如果\(p<1\)则为\(p\),如果\(p\geq1\)则为1)。构建新路径的一种朴素方法是移动一个单独的“珠子”,如左图所示。我们注意到,拟议的新路径被拒绝的概率是有限的,这意味着珠子保持在其位置。这个朴素的更新方法存在较长的关联时间,一般不用于最先进的模拟中。
多级路径积分蒙特卡罗

一种更聪明的构建新路径的方法是同时移动几个连续的“珠子”,即同时移动路径的一部分。这种方法通常被称为多级PIMC方法。左图展示了多级PIMC方法。
密度分布

最后,从模拟路径中,我们可以提取我们感兴趣的观测量。我们选择密度分布函数来说明这个过程。密度只是上图中\(x\)位置的分布。随着模拟的进行,我们通过收集位置值得到密度分布函数。左图显示了位置的直方图,即密度分布。
总结
上述电影/图像展示了单粒子在谐振子陷阱中PIMC技术的基本思想。重要的是要意识到,PIMC技术可以做更多的事情。我们可以模拟具有指定统计和任意相互作用(包括两体和三体相互作用)的多粒子系统。我们通过PIMC方法获得的结果如下:
Y. Yan and D. Blume, JPB 50, 223001 (2017)
Y. Yan and D. Blume, PRL 112, 235301 (2014)
Y. Yan and D. Blume, PRA 88, 023616 (2013)
更多
“Statistical Mechanics: Algorithms and Computations” by Werner Krauth (coursera).